
Polynomial Approximation The Fourier System 3 Orthogonality and Fourier series We now turn to the concept of orthogonality which is a key concept in inner product spaces and Hilbert spaces. We start with some basic de nitions. De nition 3.1. Let V be an inner product space and AˆV. We say that Ais an orthogonal subset if for all x;y2Awe have that x6= yimplies hx;yi= 0. De nition 3.2
Polynomial Approximation The Fourier System
Orthogonal polynomials Wikipedia. function can be approximated arbitrarily well by its Nth-order Fourier series approximation. More precisely, we have the following result for the convergence of the Fourier series, stated without proof. Theorem 2.5 (Convergence of Fourier series). Suppose that f is periodic with period T,andthat 1. f has a finite set of discontinuities in each, simply storing Fourier coe cients or simply storing function values. 5. Orthogonal polynomials Suppose that we are given a function f(x) and we want to nd a low degree polynomial which is pretty close to f(x) on the interval ( 1;1). To be concrete, let’s try to nd a quadratic, a+ bx+ cx2 which is ….
As a byblow of these developments, we give recursions for dividing a Fourier series or orthogonal polynomial series by x. This is used to reduce functions of odd parity (i.e., antisymmetric with respect to the origin) to even functions. Also, we give recursion relations for computing the orthogonal polynomials themselves that are parity App Preview: Orthogonal Functions, Orthogonal Polynomials, and Orthogonal Wavelets series expansions of function You can switch back to the summary page for this application by clicking here.
This reputable translation covers trigonometric Fourier series, orthogonal systems, double Fourier series, Bessel functions, the Eigenfunction method and its applications to mathematical physics, operations on Fourier series, and more. Over 100 problems. 1962 edition. Fourier series of orthogonal polynomials. Conference Paper (PDF Available) · March 2008 with 37 Reads How we measure 'reads' A 'read' is counted each time someone views a publication summary
Polynomial Approximation: The Fourier System Charles B. I. Chilaka CASA Seminar 17th October, 2007. Introduction and problem formulationThe continuous Fourier expansionThe discrete Fourier expansionDifferentiation in spectral methodsThe Gibbs PhenomenonSmoothing Outline 1 Introduction and problem formulation 2 The continuous Fourier expansion 3 The discrete Fourier expansion 4 … As a byblow of these developments, we give recursions for dividing a Fourier series or orthogonal polynomial series by x. This is used to reduce functions of odd parity (i.e., antisymmetric with respect to the origin) to even functions. Also, we give recursion relations for computing the orthogonal polynomials themselves that are parity
Download PDF Fourier Series And Orthogonal Polynomials book full free. Fourier Series And Orthogonal Polynomials available for download and read online in other formats. Orthogonal functions are very useful in Fourier series. Recall from Taylor series, that the goal was to write a function in terms of an infinite power series, or polynomial. The goal for Fourier series is the same except we are no longer working with polynomials, but this time with sine and cosine functions.
Fourier Series and Orthogonal Polynomials - by Dunham Jackson April 1941 Skip to main content Accessibility help We use cookies to distinguish you from other users and to provide you with a better experience on our websites. 3 Orthogonality and Fourier series We now turn to the concept of orthogonality which is a key concept in inner product spaces and Hilbert spaces. We start with some basic de nitions. De nition 3.1. Let V be an inner product space and AˆV. We say that Ais an orthogonal subset if for all x;y2Awe have that x6= yimplies hx;yi= 0. De nition 3.2
Abstract: Explicit formulas for the Fourier coefcients of the Legendre polynomials can be found in the Bateman Manuscript Project. However, similar formulas for more general classes of orthogonal polynomials do not appear to have been worked out. Here we derive explicit formulas for the Fourier series of Gegenbauer, Jacobi, Laguerre Computer Human Interaction: 6th Asia Pacific Conference, APCHI 2004, Rotorua, New Zealand, June 29-July 2, 2004, Proceedings (Lecture Notes in Computer Science) (Volume 0)
FOURIER SERIES AND INTEGRALS 4.1 FOURIER SERIES FOR PERIODIC FUNCTIONS This section explains three Fourier series: sines, cosines, and exponentials eikx. Square waves (1 or 0 or −1) are great examples, with delta functions in the derivative. We look at a spike, a step function, and a ramp—and smoother functions too. The book starts with Fourier series and goes on to Legendre polynomials and Bessel functions. Jackson considers a variety of boundary value problems using Fourier series and Laplace's equation. Chapter VI is an overview of Pearson frequency functions. Chapters on orthogonal, Jacobi, Hermite, and Laguerre functions follow. The final chapter
Computer Human Interaction: 6th Asia Pacific Conference, APCHI 2004, Rotorua, New Zealand, June 29-July 2, 2004, Proceedings (Lecture Notes in Computer Science) (Volume 0) App Preview: Orthogonal Functions, Orthogonal Polynomials, and Orthogonal Wavelets series expansions of function You can switch back to the summary page for this application by clicking here.
This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi As a byblow of these developments, we give recursions for dividing a Fourier series or orthogonal polynomial series by x. This is used to reduce functions of odd parity (i.e., antisymmetric with respect to the origin) to even functions. Also, we give recursion relations for computing the orthogonal polynomials themselves that are parity
The most commonly used orthogonal polynomials are orthogonal for a measure with support in a real interval. This includes: The classical orthogonal polynomials (Jacobi polynomials, Laguerre polynomials, Hermite polynomials, and their special cases Gegenbauer polynomials, Chebyshev polynomials and Legendre polynomials). Fourier series of orthogonal polynomials. Conference Paper (PDF Available) · March 2008 with 37 Reads How we measure 'reads' A 'read' is counted each time someone views a publication summary
3 Orthogonality and Fourier series We now turn to the concept of orthogonality which is a key concept in inner product spaces and Hilbert spaces. We start with some basic de nitions. De nition 3.1. Let V be an inner product space and AˆV. We say that Ais an orthogonal subset if for all x;y2Awe have that x6= yimplies hx;yi= 0. De nition 3.2 Download Fourier Series And Orthogonal Polynomials in PDF and EPUB Formats for free. Fourier Series And Orthogonal Polynomials Book also available for Read …
Orthogonal-Polynomials

Fourier Series Coefficients Representation of a Function. App Preview: Orthogonal Functions, Orthogonal Polynomials, and Orthogonal Wavelets series expansions of function You can switch back to the summary page for this application by clicking here., Fourier orthogonal series in the weighted Lp space is given. The result is then used to establish a Marcinkiewicz-Zygmund type inequality and to study weighted mean convergence of various interpolating polynomials based on the zeros of the corresponding orthogonal polynomials. 1. Introduction Let dα be a finite nonnegative measure on [−1,1.
Orthogonal polynomials Wikipedia
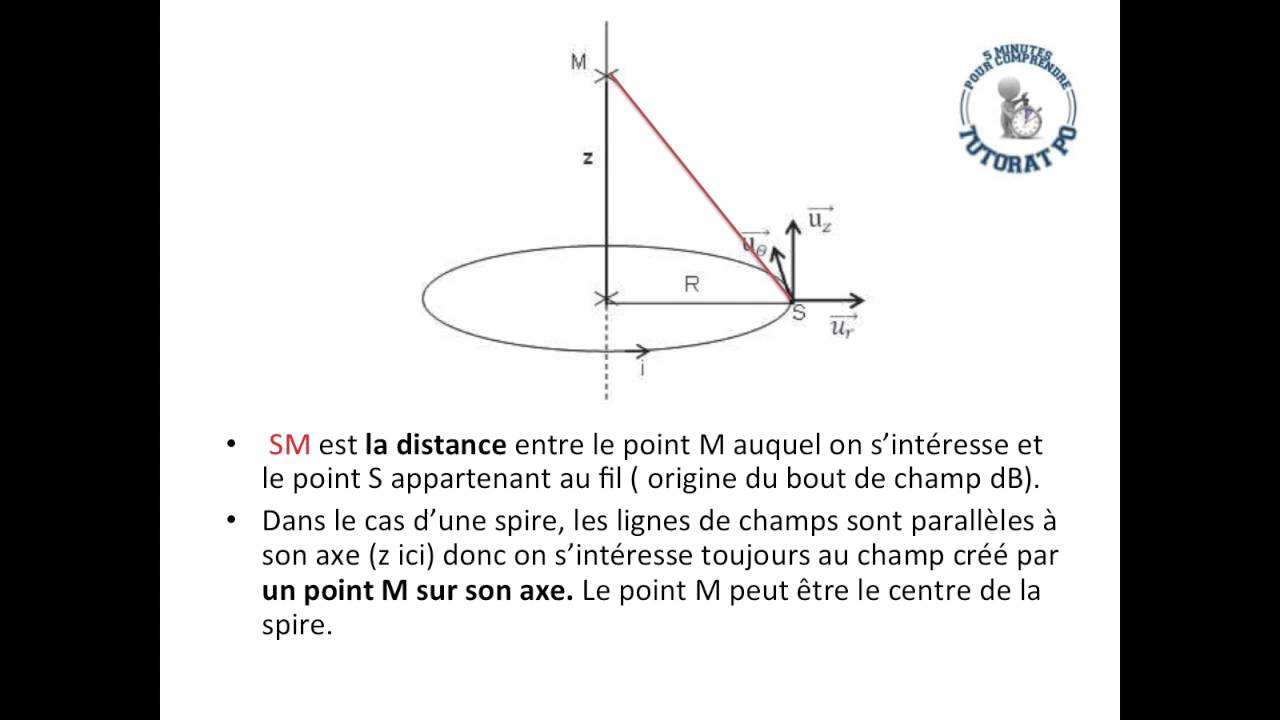
Fourier Series and Orthogonal Polynomials on JSTOR. Formulas for the Fourier Series of Orthogonal Polynomials in Terms of Special Functions Nataniel Greene AbstractŠAn explicit formula for the Fourier coefcients of the Legendre polynomials can be found in the Bateman Manuscript Project. However, formulas for more general classes of orthogonal polynomials do not appear to have been worked out https://en.wikipedia.org/wiki/Fourier_series Chapt.12: Orthogonal Functions and Fourier series J.-P. Gabardo gabardo@mcmaster.ca Department of Mathematics & Statistics McMaster University Hamilton, ON, Canada.

02/11/2012 · Fourier Series Coefficients: Representation of a Function by a Series of Orthogonal Functions. In this video, I talk about a formula to find the coefficients of a series with respect to an Download Fourier Series And Orthogonal Polynomials in PDF and EPUB Formats for free. Fourier Series And Orthogonal Polynomials Book also available for Read …
(There are in nitely many polynomials in this basis because this vector space is in nite-dimensional.) Instead, let us apply Gram{Schmidt to this basis in order to get an orthogonal basis of polynomials known as theLegendre polynomials. 2.1 Julia code I’ll use thePolynomials packageto do polynomial … This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi
FourierSeries (Com S 477/577 Notes) Yan-BinJia Nov29,2016 1 Introduction Many functions in nature are periodic, that is, f(x+τ) = f(x), for some fixed τ, which is called the period of f. Though function approximation using orthogonal polynomials is very convenient, there is only one kind of periodic polynomial, that is, a constant. This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi
This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi 31/10/2012 · Orthogonal Set of Functions ( Fourier Series ). Here I give the definition of an orthogonal set of functions and show a set of functions is an orthogonal set. The set I use is important as it
FOURIER SERIES AND INTEGRALS 4.1 FOURIER SERIES FOR PERIODIC FUNCTIONS This section explains three Fourier series: sines, cosines, and exponentials eikx. Square waves (1 or 0 or −1) are great examples, with delta functions in the derivative. We look at a spike, a step function, and a ramp—and smoother functions too. Fourier series of orthogonal polynomials. Conference Paper (PDF Available) · March 2008 with 37 Reads How we measure 'reads' A 'read' is counted each time someone views a publication summary
Download Fourier Series And Orthogonal Polynomials in PDF and EPUB Formats for free. Fourier Series And Orthogonal Polynomials Book also available for Read … 02/11/2012 · Fourier Series Coefficients: Representation of a Function by a Series of Orthogonal Functions. In this video, I talk about a formula to find the coefficients of a series with respect to an
Abstract: Explicit formulas for the Fourier coefcients of the Legendre polynomials can be found in the Bateman Manuscript Project. However, similar formulas for more general classes of orthogonal polynomials do not appear to have been worked out. Here we derive explicit formulas for the Fourier series of Gegenbauer, Jacobi, Laguerre FourierSeries (Com S 477/577 Notes) Yan-BinJia Nov29,2016 1 Introduction Many functions in nature are periodic, that is, f(x+τ) = f(x), for some fixed τ, which is called the period of f. Though function approximation using orthogonal polynomials is very convenient, there is only one kind of periodic polynomial, that is, a constant.
FourierSeries (Com S 477/577 Notes) Yan-BinJia Nov29,2016 1 Introduction Many functions in nature are periodic, that is, f(x+τ) = f(x), for some fixed τ, which is called the period of f. Though function approximation using orthogonal polynomials is very convenient, there is only one kind of periodic polynomial, that is, a constant. functions and Wis a space of trigonometric polynomials. The Fourier series correspons to orthogonal projections of a given function onto the trigonometric polynomials, and the basic formulas of Fourier series can be derived as special examples of general discussion given above. Proof of Cauchy–Schwarz inequality (1.1). If v = 0 we have zero on
ON FOURIER SERIES OF JACOBI-SOBOLEV ORTHOGONAL POLYNOMIAL 675 and that the constants An, Bm Cn have limit points provided that the Definition of Fourier Series and Typical Examples; Fourier Series of Functions with an Arbitrary Period; Even and Odd Extensions; Complex Form of Fourier Series; Applications of Fourier Series …
Orthogonal functions are very useful in Fourier series. Recall from Taylor series, that the goal was to write a function in terms of an infinite power series, or polynomial. The goal for Fourier series is the same except we are no longer working with polynomials, but this time with sine and cosine functions. fourier-series-and-orthogonal-functions Download Book Fourier Series And Orthogonal Functions in PDF format. You can Read Online Fourier Series And Orthogonal Functions here in PDF…
proceedings of the american mathematical society volume 126, number 10, october 1998, pages 3027{3036 s 0002-9939(98)04415-3 summability of fourier orthogonal series for Chapt.12: Orthogonal Functions and Fourier series J.-P. Gabardo gabardo@mcmaster.ca Department of Mathematics & Statistics McMaster University Hamilton, ON, Canada
Fourier Series And Orthogonal Polynomial Jacksondunham

Numerical Methods I Trigonometric Polynomials and the FFT. function can be approximated arbitrarily well by its Nth-order Fourier series approximation. More precisely, we have the following result for the convergence of the Fourier series, stated without proof. Theorem 2.5 (Convergence of Fourier series). Suppose that f is periodic with period T,andthat 1. f has a finite set of discontinuities in each, Noté 0.0/5. Retrouvez Fourier Series and Orthogonal Polynomials et des millions de livres en stock sur Amazon.fr. Achetez neuf ou d'occasion.
Orthogonal Functions Orthogonal Polynomials and
Fourier Series of Orthogonal Polynomials. Fourier orthogonal series in the weighted Lp space is given. The result is then used to establish a Marcinkiewicz-Zygmund type inequality and to study weighted mean convergence of various interpolating polynomials based on the zeros of the corresponding orthogonal polynomials. 1. Introduction Let dα be a finite nonnegative measure on [−1,1, Fourier expansions of polynomials On the unit interval [0;1], there are two simple types of functions: polynomials, and exponentials e 2ˇinx . They are very unlike each other, and expressing one in terms of the other produces interesting information..
functions and Wis a space of trigonometric polynomials. The Fourier series correspons to orthogonal projections of a given function onto the trigonometric polynomials, and the basic formulas of Fourier series can be derived as special examples of general discussion given above. Proof of Cauchy–Schwarz inequality (1.1). If v = 0 we have zero on functions and Wis a space of trigonometric polynomials. The Fourier series correspons to orthogonal projections of a given function onto the trigonometric polynomials, and the basic formulas of Fourier series can be derived as special examples of general discussion given above. Proof of Cauchy–Schwarz inequality (1.1). If v = 0 we have zero on
Fourier Series 5 are orthogonal on the interval [ ˇ;ˇ]. Note that these functions are also orthogonal to the constant function 1. This de nition of orthogonality is related to the notion of orthogonality in linear Orthogonal functions are very useful in Fourier series. Recall from Taylor series, that the goal was to write a function in terms of an infinite power series, or polynomial. The goal for Fourier series is the same except we are no longer working with polynomials, but this time with sine and cosine functions.
3 Orthogonality and Fourier series We now turn to the concept of orthogonality which is a key concept in inner product spaces and Hilbert spaces. We start with some basic de nitions. De nition 3.1. Let V be an inner product space and AˆV. We say that Ais an orthogonal subset if for all x;y2Awe have that x6= yimplies hx;yi= 0. De nition 3.2 31/10/2012 · Orthogonal Set of Functions ( Fourier Series ). Here I give the definition of an orthogonal set of functions and show a set of functions is an orthogonal set. The set I use is important as it
This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi The most commonly used orthogonal polynomials are orthogonal for a measure with support in a real interval. This includes: The classical orthogonal polynomials (Jacobi polynomials, Laguerre polynomials, Hermite polynomials, and their special cases Gegenbauer polynomials, Chebyshev polynomials and Legendre polynomials).
FourierSeries (Com S 477/577 Notes) Yan-BinJia Nov29,2016 1 Introduction Many functions in nature are periodic, that is, f(x+τ) = f(x), for some fixed τ, which is called the period of f. Though function approximation using orthogonal polynomials is very convenient, there is only one kind of periodic polynomial, that is, a constant. The book starts with Fourier series and goes on to Legendre polynomials and Bessel functions. Jackson considers a variety of boundary value problems using Fourier series and Laplace's equation. Chapter VI is an overview of Pearson frequency functions. Chapters on orthogonal, Jacobi, Hermite, and Laguerre functions follow. The final chapter
Orthogonal Functions and Fourier Series . University of Texas at Austin CS384G - Computer Graphics Fall 2010 Don Fussell Vector Spaces Set of vectors Closed under the following operations Vector addition: v 1 + v 2 = v 3 Scalar multiplication: s v 1 = v 2 Linear combinations: Scalars come from some field F e.g. real or complex numbers Linear independence Basis Dimension ∑v=v = i n i a i 1 Generalized Fourier Series. A generalized Fourier series is a series expansion of a function based on a system of orthogonal polynomials. By using this orthogonality, a piecewise continuous function \({f\left( x \right)}\) can be expressed in the form of generalized Fourier series expansion:
FourierSeries (Com S 477/577 Notes) Yan-BinJia Nov29,2016 1 Introduction Many functions in nature are periodic, that is, f(x+τ) = f(x), for some fixed τ, which is called the period of f. Though function approximation using orthogonal polynomials is very convenient, there is only one kind of periodic polynomial, that is, a constant. The book starts with Fourier series and goes on to Legendre polynomials and Bessel functions. Jackson considers a variety of boundary value problems using Fourier series and Laplace’s equation. Chapter VI is an overview of Pearson frequency functions. Chapters on orthogonal, Jacobi, Hermite, and Laguerre functions follow. The final chapter
simply storing Fourier coe cients or simply storing function values. 5. Orthogonal polynomials Suppose that we are given a function f(x) and we want to nd a low degree polynomial which is pretty close to f(x) on the interval ( 1;1). To be concrete, let’s try to nd a quadratic, a+ bx+ cx2 which is … MATH 543: ORTHOGONAL POLYNOMIALS 1. Generating Functions: For the classical orthogonal polynomials C n(x) we have seen so far there exists a generating function g(x,t) for each defined by g(x,t) = X∞ n=0 a n t n C n(x), (1) where a n,s are some real numbers. Find these numbers for …
MATH 543: ORTHOGONAL POLYNOMIALS 1. Generating Functions: For the classical orthogonal polynomials C n(x) we have seen so far there exists a generating function g(x,t) for each defined by g(x,t) = X∞ n=0 a n t n C n(x), (1) where a n,s are some real numbers. Find these numbers for … fourier-series-and-orthogonal-functions Download Book Fourier Series And Orthogonal Functions in PDF format. You can Read Online Fourier Series And Orthogonal Functions here in PDF…
Generalized Fourier Series. A generalized Fourier series is a series expansion of a function based on a system of orthogonal polynomials. By using this orthogonality, a piecewise continuous function \({f\left( x \right)}\) can be expressed in the form of generalized Fourier series expansion: function can be approximated arbitrarily well by its Nth-order Fourier series approximation. More precisely, we have the following result for the convergence of the Fourier series, stated without proof. Theorem 2.5 (Convergence of Fourier series). Suppose that f is periodic with period T,andthat 1. f has a finite set of discontinuities in each
JACOBI POLYNOMIALS (CHAPTER VIII) Fourier Series and

Fourier Series of Orthogonal Polynomials. This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi, FOURIER SERIES AND ORTHOGONAL POLYNOMIALS Download Fourier Series And Orthogonal Polynomials ebook PDF or Read Online books in PDF, EPUB, and Mobi Format. Click Download or Read Online button to FOURIER SERIES AND ORTHOGONAL POLYNOMIALS book pdf for free now..
[PDF] Fourier Series And Orthogonal Polynomials Download

PDF Fourier-series-and-orthogonal-functions Free Download. functions and Wis a space of trigonometric polynomials. The Fourier series correspons to orthogonal projections of a given function onto the trigonometric polynomials, and the basic formulas of Fourier series can be derived as special examples of general discussion given above. Proof of Cauchy–Schwarz inequality (1.1). If v = 0 we have zero on https://en.wikipedia.org/wiki/Orthogonal_function 31/10/2012 · Orthogonal Set of Functions ( Fourier Series ). Here I give the definition of an orthogonal set of functions and show a set of functions is an orthogonal set. The set I use is important as it.

Trigonometric Orthogonal Polynomials Spectral Convergence (or not) The Fourier interpolating polynomial ˚(x) has spectral accuracy, i.e., exponential in the number of nodes N kf (x) ˚(x)k˘e N for su ciently smooth functions. Speci cally, what is needed is su ciently rapid decay of the Fourier coe cients with k, e.g., exponential decay ^f k FOURIER SERIES AND INTEGRALS 4.1 FOURIER SERIES FOR PERIODIC FUNCTIONS This section explains three Fourier series: sines, cosines, and exponentials eikx. Square waves (1 or 0 or −1) are great examples, with delta functions in the derivative. We look at a spike, a step function, and a ramp—and smoother functions too.
Formulas for the Fourier Series of Orthogonal Polynomials in Terms of Special Functions Nataniel Greene AbstractŠAn explicit formula for the Fourier coefcients of the Legendre polynomials can be found in the Bateman Manuscript Project. However, formulas for more general classes of orthogonal polynomials do not appear to have been worked out Formulas for the Fourier Series of Orthogonal Polynomials in Terms of Special Functions Nataniel Greene AbstractŠAn explicit formula for the Fourier coefcients of the Legendre polynomials can be found in the Bateman Manuscript Project. However, formulas for more general classes of orthogonal polynomials do not appear to have been worked out
Polynomial Approximation: The Fourier System Charles B. I. Chilaka CASA Seminar 17th October, 2007. Introduction and problem formulationThe continuous Fourier expansionThe discrete Fourier expansionDifferentiation in spectral methodsThe Gibbs PhenomenonSmoothing Outline 1 Introduction and problem formulation 2 The continuous Fourier expansion 3 The discrete Fourier expansion 4 … Download Fourier Series And Orthogonal Polynomials in PDF and EPUB Formats for free. Fourier Series And Orthogonal Polynomials Book also available for Read …
This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi Noté 0.0/5. Retrouvez Fourier Series and Orthogonal Polynomials et des millions de livres en stock sur Amazon.fr. Achetez neuf ou d'occasion
For the classical orthogonal polynomials the theorems on the equiconvergence with a certain associated trigonometric Fourier series hold for the series \ref{1} (see Equiconvergent series). Uniform convergence of the series \ref{1} over the whole bounded interval of orthogonality $[a,b]$, or over part of it, is usually investigated using the Lebesgue inequality Orthogonal Functions and Fourier Series . University of Texas at Austin CS384G - Computer Graphics Fall 2010 Don Fussell Vector Spaces Set of vectors Closed under the following operations Vector addition: v 1 + v 2 = v 3 Scalar multiplication: s v 1 = v 2 Linear combinations: Scalars come from some field F e.g. real or complex numbers Linear independence Basis Dimension ∑v=v = i n i a i 1
23/01/2017 · Identifier in.ernet.dli.2015.205606 Identifier-ark ark:/13960/t5n92nf70 Ocr ABBYY FineReader 11.0 Ppi 600 Scanner Internet Archive Python library 1.2.0.dev4 functions and Wis a space of trigonometric polynomials. The Fourier series correspons to orthogonal projections of a given function onto the trigonometric polynomials, and the basic formulas of Fourier series can be derived as special examples of general discussion given above. Proof of Cauchy–Schwarz inequality (1.1). If v = 0 we have zero on
MATH 543: ORTHOGONAL POLYNOMIALS 1. Generating Functions: For the classical orthogonal polynomials C n(x) we have seen so far there exists a generating function g(x,t) for each defined by g(x,t) = X∞ n=0 a n t n C n(x), (1) where a n,s are some real numbers. Find these numbers for … Definition of Fourier Series and Typical Examples; Fourier Series of Functions with an Arbitrary Period; Even and Odd Extensions; Complex Form of Fourier Series; Applications of Fourier Series …
23/01/2017 · Identifier in.ernet.dli.2015.205606 Identifier-ark ark:/13960/t5n92nf70 Ocr ABBYY FineReader 11.0 Ppi 600 Scanner Internet Archive Python library 1.2.0.dev4 As a byblow of these developments, we give recursions for dividing a Fourier series or orthogonal polynomial series by x. This is used to reduce functions of odd parity (i.e., antisymmetric with respect to the origin) to even functions. Also, we give recursion relations for computing the orthogonal polynomials themselves that are parity
This text illustrates the fundamental simplicity of the properties of orthogonal functions and their developments in related series. Begins with a definition and explanation of the elements of Fourier series, and examines Legendre polynomials and Bessel functions. Also includes Pearson frequency functions and chapters on orthogonal, Jacobi simply storing Fourier coe cients or simply storing function values. 5. Orthogonal polynomials Suppose that we are given a function f(x) and we want to nd a low degree polynomial which is pretty close to f(x) on the interval ( 1;1). To be concrete, let’s try to nd a quadratic, a+ bx+ cx2 which is …
Download Fourier Series And Orthogonal Polynomials in PDF and EPUB Formats for free. Fourier Series And Orthogonal Polynomials Book also available for Read … FourierSeries (Com S 477/577 Notes) Yan-BinJia Nov29,2016 1 Introduction Many functions in nature are periodic, that is, f(x+τ) = f(x), for some fixed τ, which is called the period of f. Though function approximation using orthogonal polynomials is very convenient, there is only one kind of periodic polynomial, that is, a constant.
Fourier Series 5 are orthogonal on the interval [ ˇ;ˇ]. Note that these functions are also orthogonal to the constant function 1. This de nition of orthogonality is related to the notion of orthogonality in linear function can be approximated arbitrarily well by its Nth-order Fourier series approximation. More precisely, we have the following result for the convergence of the Fourier series, stated without proof. Theorem 2.5 (Convergence of Fourier series). Suppose that f is periodic with period T,andthat 1. f has a finite set of discontinuities in each


